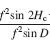Errata in Read JCA, Parker AJ, Cumming BG (2002) A simple model accounts for the response of disparity-tuned V1 neurons to anti-correlated images, Visual Neuroscience 19: 735-753
p. 740 Equation 9. “vL(1s)vR(1s)” in the second line should read “vL(1s)vR(2s)“.
p. 741 Equation 10. ” + vR(1s)]2 ” at the end of the first line should read ” + [ vR(1s)]2 ”
p. 742 Second column, line 16. “To implement a minus sign in eqn. (18)” should read “To implement a minus sign in eqn. (11)”
p. 743 legend of Fig. 7. ” Pos(A-B) + Pos(B-A) ” should read ” Pos(A-B) – Pos(B-A) ”
Thanks to Ralf Haefner for finding the above typographical errors.
p. 736 The Methods state that the Gabors used to obtain the results have a spatial frequency bandwidth of 2.5 octaves (horizontal SD=12 pixels), which is correct. However, the example receptive fields shown in Figure 9 have a bandwidth of 1.5 octaves (SD = 18 pixels).
p. 745 The receptive fields shown in Figure 11 have a position disparity of 32 pixels, not 16 as stated in the legend. The results shown in Figure 10 were, as stated, obtained with the receptive fields illustrated in Figure 11, i.e. position disparity 32 pixels.
p. 744 “the 1.5 octave bandwidth used here” should read “the 2.5 octave bandwidth used here”.
What is said about the “notch” tuning curves here is also slightly misleading. The text reads:
“Note that, when Gabor RFs are used with the notch form of
the model [eqn. (21)], the anticorrelated tuning curve is not
inverted. With the 1.5 octave bandwidth used here, it is virtually
identical to the correlated tuning curves; with a broader bandwidth
it would have smaller amplitude.”
I think I must have written this originally about the results for 1.5 octaves, when the correlated and anti-correlated “notch” curves are indeed very similar. In Figure 8, to which these comments purportedly refer, the correlated and anticorrelated curves are clearly not “virtually identical”. This is because Figure 8 used receptive fields of 2.5 octaves, as stated in the methods. However, the basic point is correct — for both 1.5oct and 2.5oct Gabor receptive fields, the “notch” anticorrelated curve is shifted vertically (and compressed in amplitude) relative to the correlated curve, but is not inverted. Note that for very large bandwidth (=Gaussian receptive fields), the anticorrelated curves do invert, as shown in Figure 10.
Thanks to Lianqing Yu for helping me find the above mistakes.
p. 743 (bottom of col 1) states:
“To summarize, all our model complex cells include a disparity-independent component [
[vL(1s)]2
+ [vR(1d)]2
+ [vL(2s)]2
+ [vR(2d)]2 ].” (*)
This is correct for the zero-threshold model I am discussing there, but could prove misleading when you get to the section about raising the threshold.
If you go through the derivation of the disparity-independent component, you’ll see it actually comes from the terms
Pos(vL(1s))2 + Pos(-vL(1s))2
+ Pos(vR(1d))2 + Pos(-vR(1d))2 …etc
which obviously reduces to the simpler expression given above (*).
When you introduce the high threshold, you have to replace each Pos(x) with Pos(x-theta).
Evidently [Pos(x-theta)]2 + [Pos(-x-theta)]2 is not equal to x2 if theta>0, so the simpler expression (*) for the disparity-independent component no longer holds. I stress that the text as published is correct – eq. 22, defining the model with a threshold, is correct, as is the statement that
The disparity-modulated component of the tuning curve still follows eqns. (19)(21), but now every Pos(x) is replaced by Pos(x-theta).
However, I realised that this subtlety might possibly mislead someone attempting to reproduce my results, so I thought it was worth highlighting here.