Gamma correction is the process of calibrating the luminance of the display, so that you can precisely control the luminance on the screen. The projectors’ images are made up of three colours: red, blue and green. To control the appearance of each pixel, you can set the level of each colour between 0 (dimmest) and 255 (brightest). Since my stimuli are all monochrome, I’ll assume all 3 colours are going to be set to the same level, and talk as if the projector had a single, white beam. I’ll talk about the “pixel value” as going from 0 (“black”) to 255 (“white”).I would like to ensure that the response is linear: i.e. doubling the pixel-value(say, from 32 to 64) results in a doubling of the rate at which photons are emitted. In general, this will not be the case when the projector arrives from the factory. For CRT monitors, the luminance is generally a power-law function of pixel value:

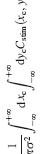
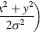luminance L = Lmin + (Lmax-Lmin) [( p – black ) / (white – black) ] ^gamma      — Eq 1

where L = measured luminance, p = pixel-value, Lmin = luminance measured when the pixel value is set to black, ie 0, and Lmax = luminance measured when the pixel value is set to white, ie 255. (I have tried to be general, rather than assuming white=255, since one day I would like to get a graphics card with more levels). gamma is the exponent describing how fast the luminance rises as a function of pixel-value — hence the term gamma function. I’ll call Eq 1 a gamma function. I would like to make gamma = 1 (linearity).

Why gamma-correct

Obviously accurate gamma correction is massively important if you are trying to probe subtle contrast non-linearities in human vision. For my purposes, it isn’t totally critical, as my stimuli at the moment are typically random-dot patterns which just consist of black and white dots on a grey background. Potentially, it could affect the anti-aliasing which I use to mimic sub-pixel displacements. Suppose I have a white dot (255) on a black background (0); I I can mimic shifting that dot one quarter of a pixel to the left by painting all the pixels to the immediate left of the dot dark gray (64). If my system isn’t linearised, that 64 that I asked for may come out not 1/4 of the white level, but 1/8th, say. In other words my dot is actually shifted 1/8th of a pixel, not 1/4. So poor gamma correction can introduce disparity artefacts (admittedly at the sub-pixel level). On the other hand, in this example even a factor of 2 error in the requested luminance causes a disparity artefact of only 1/8 pixel, or 0.3 arcmin. It’s good that highly accurate linearity isn’t critical for me, because as you’ll see my projectors do not allow me to achieve it.